CF2122-总结

First Post:

Last Update:

Word Count:
4.4k

Read Time:
20 min

Page View: loading...

CF2122-总结

A

翻译

在一个 的每一个格子中包含一个非负数的网格中，称一条路径是 down/right 的，当且仅当这条路径从左上角格子开始，且其中的每一步要么向右一格，要么向下一格。称一条路径是 greedy 的，当且仅当这条路径满足以下条件：

  • 这条路径是 down/right 路径
  • 如果当前格子右边的数比下边的大，那么一定向右。如果当前格子下边的数比右边的大，那么一定向下。（若有一边没有格子或两侧相等，则无限制。）

定义一条路径的权值是其经过的所有格子上的数的总和。对于给定的 ，求是否存在一个 的网格使得每条 greedy 的路径都不是权值最大的 down/right 路径。 组数据。

题解

容易发现 的网格， 的网格中 greedy 路径一定是权值最大的。这些情况下答案是 NO。

对于 的网格，有以下构造。

更大的情况是类似的。答案一定是 YES。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<bits/stdc++.h>
#define f(i,x,y) for(int i=x, i##end=y; i<=i##end; ++i)
#define d(i,x,y) for(int i=y, i##end=x; i>=i##end; --i)
#define uf(i,x,y) for(int i=x, i##end=y; i<i##end; ++i)
#define ll long long
#define pir pair<int, int>
#define fir first
#define sec second
#define mp make_pair
#define pb push_back 
char ch;
int rd() {
	int f=1, x=0; ch=getchar();
	while(!isdigit(ch)) { f=((ch=='-')?-1:f); ch=getchar(); }
	while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar(); }
	return x*f;
}
void rd(int& x) { x=rd(); }
using namespace std;
int main() {
	int t = rd(); while(t--) {
		int n = rd(), m = rd();
		cout << ((((n <= 2) && (m <= 2)) || (n == 1) || (m == 1)) ? ("NO") : ("YES")) << endl;
	}
	return 0;
}

B

翻译

给定 个 piles。第 个 pile 从上到下由 个 0 和 个 1 组成。一次操作是从某个 pile 的最上方取走一个数，将其插入任意一个 pile 的任意位置。

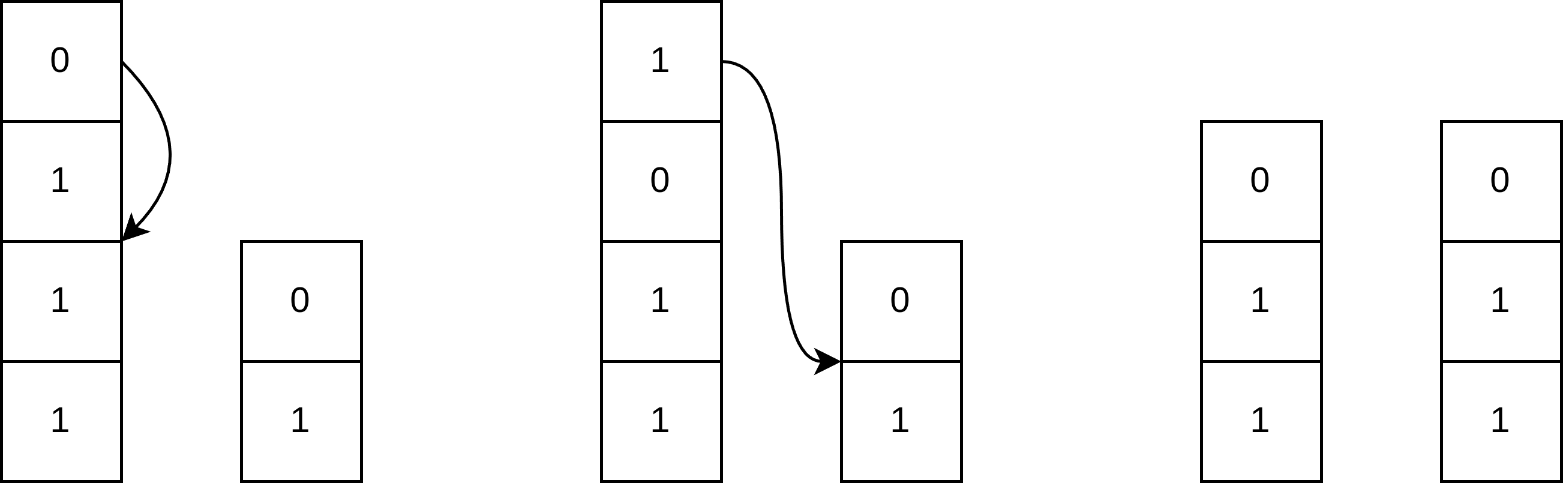
给定 , 。欲通过若干次操作使得 ，第 堆石子都变为从上到下由 个 0 和 和 1 组成。求最少使用多少次操作。

， 组数据，保证 。

题解

若某一个 pile 需要移走若干个 1，则这些 1 上面的 0 必须先全部被移走。若某一 pile 中 且 ，则我们必须先将这些 0 移走。样例提醒我们我们可以往本堆的下面放来把一些 1 暴露在最上面，这样可以把这些多余的 1 移给别的缺少的堆的。这样做需要 步。容易证明这样做步数是最少的。

如果某一 pile 中 且 ，那么同理我们必须把这些 0 移走。不同的是，我们只将后 个石子移到本堆的下面。这样做也需要 步。容易证明这样做步数是最少的。同样，如果某一 pile 中 ，那么至少需要 步。

发现每一个下界都能达到。直接统计即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
#define f(i,x,y) for(int i=x, i##end=y; i<=i##end; ++i)
#define d(i,x,y) for(int i=y, i##end=x; i>=i##end; --i)
#define uf(i,x,y) for(int i=x, i##end=y; i<i##end; ++i)
#define ll long long
#define pir pair<int, int>
#define fir first
#define sec second
#define mp make_pair
#define pb push_back 
char ch;
int rd() {
	int f=1, x=0; ch=getchar();
	while(!isdigit(ch)) { f=((ch=='-')?-1:f); ch=getchar(); }
	while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar(); }
	return x*f;
}
void rd(int& x) { x=rd(); }
using namespace std;
void solve() {
	int n = rd(); ll ans = 0;
	for(int i = 1; i <= n; ++i) {
		int a = rd(), b = rd(), c = rd(), d = rd();
		if(b > d) ans += (a + b - d);
		else if(a > c) ans += (a - c);
	}
	cout << ans << endl;
}
int main() {
	int t = rd(); while(t--) {
		solve();
	}
	return 0;
}

C

翻译

给定 个平面上的点 。选出 个点对（每个点不被重复选择），最大化这些点对间曼哈顿距离的和，输出方案。 组数据，保证 。

题解

考虑按 排序所有点。找一条线尽可能平分左右的点。发现左边的点一定不会和左边的点匹配，右边的点亦然。若否，则必可以在左右各找到一个内部匹配的点对，进行交换一定使答案增大。

因此，左边的点一定和右边的某个点匹配。所以 坐标维度上，左边的点 一定贡献 ，右边的点 一定贡献 。因此我们可以不考虑 维度。

不妨考虑 的情况。问题变成了给定两个数列 和 ，找一个配对方案最大化组内 与 差的绝对值。容易发现两两排序，让小的匹配大的即可（证明和上面的类似）。

的情况，点多的那边必然有一个点未被匹配。枚举未被匹配的点，其它点依然是按顺序匹配的。容易发现每个点最多和某两个另一侧的点匹配，且必定只有某个后缀是匹配前一个另一侧节点的。前缀和维护即可快速计算某个点未被匹配情况下的答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
#define f(i,x,y) for(int i=x, i##end=y; i<=i##end; ++i)
#define d(i,x,y) for(int i=y, i##end=x; i>=i##end; --i)
#define uf(i,x,y) for(int i=x, i##end=y; i<i##end; ++i)
#define ll long long
#define pir pair< pair<int, int>, int >
#define fir first.first
#define sec first.second
#define thr second
#define mp make_pair
#define pb push_back 
char ch;
int rd() {
	int f=1, x=0; ch=getchar();
	while(!isdigit(ch)) { f=((ch=='-')?-1:f); ch=getchar(); }
	while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar(); }
	return x*f;
}
void rd(int& x) { x=rd(); }
using namespace std;
const int _ = 200005;
pir P[_]; int n;
int calc(pir x, pir y) {
	return abs(x.fir - y.fir) + abs(x.sec - y.sec);
}
ll tans[_][2];
void solve() {
	rd(n); f(i,1,n) { rd(P[i].fir); rd(P[i].sec); P[i].thr = i; }
	sort(P+1, P+1+n) ;
	ll ans = 0; int ansi = 0;
	if(!(n&1)) { // all dots are chosen
		int p = n/2;
		sort(P+1, P+p+1, [](pir x, pir y){return x.sec < y.sec;});
		sort(P+p+1, P+n+1, [](pir x, pir y){return x.sec > y.sec;});
		f(i,1,p) ans += calc(P[i], P[p + i]);
		f(i,1,p) cout << P[i].thr << ' ' << P[p + i].thr << '\n';
		// cerr << "Ans = " << ans << endl;
	} else { // one dot is not chosen
		int p = n/2; //[1, p], [p+1, n]
		sort(P+1, P+p+1, [](pir x, pir y){return x.sec < y.sec;});
		sort(P+p+1, P+n+1, [](pir x, pir y){return x.sec > y.sec;});
		memset(tans, 0, sizeof(tans));
		f(i,1,p+1) {
			tans[i][0] = calc(P[p + i], P[i]), tans[i][1] = calc(P[p + i], P[i-1]);
			tans[i][0] += tans[i-1][0]; tans[i][1] += tans[i-1][1];
		}
		f(i,1,p+1) {
			if(ans < tans[i-1][0] + tans[p+1][1] - tans[i][1]) ans = tans[i-1][0] + tans[p+1][1] - tans[i][1], ansi = i ;
		}
		f(i,1,p+1) {
			if(i < ansi) cout << P[p + i].thr << ' ' << P[i].thr << '\n';
			if(i > ansi) cout << P[p + i].thr << ' ' << P[i-1].thr << '\n';
		}
		// cerr << "Ans = " << ans << endl;
	}
}
int main() {
	int t = rd(); while(t--) {
		solve();
	}
	return 0;
}

D

翻译

给定一个 个点 条边的无向图。一个 token 第 秒时在 1 号节点。在第 秒时，如果 token 在 号节点上，则可以从以下两个操作中选择一个执行：

  • 在原地等待 秒。
  • 花费 时间通过 节点的第 条边。

其中， 节点的第 条边指按照输入顺序，包含 节点的第 条边。求到达 号点的最小时间，以及最小化这一时间的前提下的最小等待时间。 组数据，保证 。

题解

猜测最小所需时间的最大值不会很多，因为如果一个节点的度数很小，那么无论往哪走等待时间都很小。如果一个节点的度数很大，那么虽然我们在这个节点可能要等很久，但是我们可以选择的节点数量也很多。可以证明所需时间的最小值是 量级的（用路径上节点 的总和作为所需时间的上界，参见这一结论）。那么枚举时间，更新可达性，把最小等待时间记录在每个节点上一起更新即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<bits/stdc++.h>
#define f(i,x,y) for(int i=x, i##end=y; i<=i##end; ++i)
#define d(i,x,y) for(int i=y, i##end=x; i>=i##end; --i)
#define uf(i,x,y) for(int i=x, i##end=y; i<i##end; ++i)
#define ll long long
#define pir pair<int, int>
#define fir first
#define sec second
#define mp make_pair
#define pb push_back 
char ch;
int rd() {
	int f=1, x=0; ch=getchar();
	while(!isdigit(ch)) { f=((ch=='-')?-1:f); ch=getchar(); }
	while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar(); }
	return x*f;
}
void rd(int& x) { x=rd(); }
using namespace std;
const int _ = 5005, inf = 0x3f3f3f3f;
int mwt[_], tmp[_], ok[_];
vector<int> edge[_]; int n, m;
void solve() {
	f(i,1,n) edge[i].clear(), ok[i] = 0, mwt[i] = inf;
	ok[1] = 1; mwt[1] = 0; rd(n); rd(m); f(i,1,m) {
		int u = rd(), v = rd();
		edge[u].pb(v); edge[v].pb(u);
	}
	for(int tim = 0; ;  ++tim) {
		// cerr << "at tim " << tim << endl;
		vector<int> L;
		f(i,1,n) { if(ok[i]) L.pb(i); tmp[i] = inf; }
		for(auto i : L) if(edge[i].size()) {
			int ver = edge[i][tim % edge[i].size()] ;
			ok[ver] = 1;
			tmp[ver] = min(tmp[ver], mwt[i]);
			// cerr << "set ok " << edge[i][tim % edge[i].size()] << endl;
		}
		f(i,1,n) mwt[i] = min(mwt[i] + 1, tmp[i]);
		if(ok[n]) { cout << tim + 1 << ' ' << mwt[n] << endl; break; }
	}
}
int main() {
	int t = rd(); while(t--) {
		solve();
	}
	return 0;
}

E

题意

在一个 的每一个格子中包含一个不大于 的正整数的网格中，称一条路径是 down/right 的，当且仅当这条路径从左上角格子开始，且其中的每一步要么向右一格，要么向下一格。称一条路径是 greedy 的，当且仅当这条路径满足以下条件：

  • 这条路径是 down/right 路径
  • 如果当前格子右边的数比下边的大，那么一定向右。如果当前格子下边的数比右边的大，那么一定向下。（若有一边没有格子或两侧相等，则无限制。）

定义一条路径的权值是其经过的所有格子上的数的总和。给定一个 的网格，其中有一些位置没有数（用 -1 表示）。求有多少种方式填充满这一网格，且对于每个子矩形，必定有一条 greedy 的路径的权值是所有 down/right 的路径中权值最大的。

题解

以下称 对于每个子矩形，必定有一条 greedy 的路径的权值是所有 down/right 的路径中权值最大的 为限制 A。

的子矩形中限制 A 一定满足。不妨假设我们从某个 矩形的左上角开始走，如果下一步是向右走，我们就变成了另一个矩形，可以不作考虑。如果往下走，我们到任意一个第二行的点的 greedy 的路径是确定的，也就是先向下然后一直向右。这启发我们将所有限制在所有满足 的 处考虑。容易发现这样的 给出的限制是 。不妨移去第一行第一个数和最后一行最后一个数，容易证明它们不会影响限制（需要注意的是，如果移去了 -1，需要在最后的答案中乘上一个 ）。

此时我们的限制变成了这样的形式：对于所有 ，如果 ，那么 ，也就是 。容易发现最靠后的限制永远是最紧的。因此只需要留存一个限制。

进行动态规划的尝试。我们可以设计一个状态 储存现在的 ，当 增加到 时，我们只需要考虑新的 和 。如果 ，我们更新 即可。否则，我们直接让限制缩小 。因此，我们记 为如果 对当前的限制为 , 把 填满的合法方案数。已经可以完成转移，但还有初始无限制的情况不能直接使用 ，否则第二维会过大。因此再设 为 无限制，把 填满的方案数。 和 都确定的情况转移是容易的。否则直接枚举新的 和 并转移。最坏时间复杂度 。使用前缀和优化 和 都是 -1 的情况即可做到 复杂度，足以通过。可以优化到 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include<bits/stdc++.h>
#define f(i,x,y) for(int i=x, i##end=y; i<=i##end; ++i)
#define d(i,x,y) for(int i=y, i##end=x; i>=i##end; --i)
#define uf(i,x,y) for(int i=x, i##end=y; i<i##end; ++i)
#define ll long long
#define pir pair<int, int>
#define fir first
#define sec second
#define mp make_pair
#define pb push_back 
char ch;
int rd() {
	int f=1, x=0; ch=getchar();
	while(!isdigit(ch)) { f=((ch=='-')?-1:f); ch=getchar(); }
	while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar(); }
	return x*f;
}
void rd(int& x) { x=rd(); }
using namespace std;
const int _ = 505, mod = 998244353;
int a[2][_], n, k, ans;
int modadd(int a, int b) {
	return (a + b > mod) ? (a + b - mod) : (a + b);
}
int modminu(int a, int b) {
	return (a - b < 0) ? (a - b + mod) : (a - b);
}
int f[_][_], g[_], s[_];
void solve() {
	rd(n); rd(k); n = n - 1; int tmp = 1;
	if(rd() == -1) tmp *= k; f(i,1,n) rd(a[0][i]);
	f(i,1,n) rd(a[1][i]); if(rd() == -1) tmp *= k;
	memset(f, 0, sizeof(f)); memset(g, 0, sizeof(g));
	g[n+1] = 1; f(i,0,k) f[n+1][i] = 1;
	d(i,1,n) {
		if((a[0][i] != -1) && (a[1][i] != -1)) {
			int x = a[0][i], v = a[1][i];
			if(x >= v) { f(j,x-v,k) f[i][j] = modadd(f[i][j], f[i+1][j - (x - v)]); g[i] = modadd(g[i], g[i+1]); }
			if(v > x) { f(j,0,k) f[i][j] = modadd(f[i][j], f[i+1][v - x]); g[i] = modadd(g[i], f[i+1][v - x]); }
		}

		if((a[0][i] != -1) && (a[1][i] == -1)) {
			int x = a[0][i] ;
			f(v,1,k) {
				if(x >= v) { f(j,x-v,k) f[i][j] = modadd(f[i][j], f[i+1][j - (x - v)]); g[i] = modadd(g[i], g[i+1]); }
				if(v > x) { f(j,0,k) f[i][j] = modadd(f[i][j], f[i+1][v - x]); g[i] = modadd(g[i], f[i+1][v - x]); }
			}
		}

		if((a[0][i] == -1) && (a[1][i] != -1)) {
			int v = a[1][i] ;
			f(x,1,k) {
				if(x >= v) { f(j,x-v,k) f[i][j] = modadd(f[i][j], f[i+1][j - (x - v)]); g[i] = modadd(g[i], g[i+1]); }
				if(v > x) { f(j,0,k) f[i][j] = modadd(f[i][j], f[i+1][v - x]); g[i] = modadd(g[i], f[i+1][v - x]); }
			}
		}

		if((a[0][i] == -1) && (a[1][i] == -1)) {
			s[0] = f[i+1][0]; f(j,1,k) s[j] = modadd(s[j-1], f[i+1][j]);
			f(v,1,k) {
				int bd = k - v;
				f(j,0,k) {
					f[i][j] = modadd(f[i][j], modminu(s[v-1], s[0])) ;
					if(j <= bd) f[i][j] = modadd(f[i][j], s[j]);
					if(j > bd) f[i][j] = modadd(f[i][j], modminu(s[j], s[j - bd - 1])) ;
				}
				f(x,1,k) {
					if(x >= v) g[i] = modadd(g[i], g[i+1]);
					if(v > x) g[i] = modadd(g[i], f[i+1][v - x]);
				}
			}
		}
	}
	ans = g[1] ;
	cout << 1LL * tmp * ans % mod << endl;
}
int main() {
	int t = rd(); while(t--) solve();
	return 0;
}

F

题意

给定 和 个正整数 。构造一个 个点的多边形，其三角剖分数量恰好是

多边形可以按照顺时针方向或逆时针方向给出。各坐标必须是 间的整数。多边形的两条共点边可以共线。多边形不必是凸的。

题解

看到这个 第一眼想到的就是它就是 。因此想到组合数。考虑能否构造出三角剖分数量恰好是 的多边形。

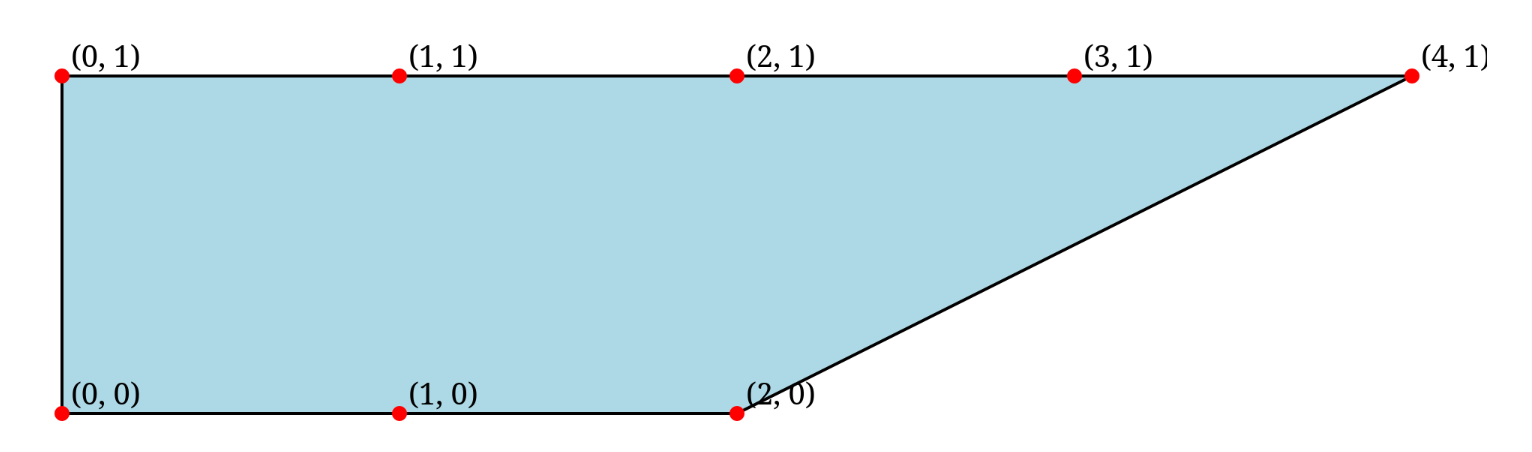
“很容易”想到在一边上放 个点，另一条边上放 个点，类似这样就可以构造出一个满足条件的多边形（例图来自官方题解）：

如图是一个恰有 种三角剖分的多边形

证明可以考虑下面最右的节点包含在哪个三角剖分内，然后列出递推式，发现等同于组合数。

考虑如何合并多个这样的多边形。想到通过构造让三角剖分除这些多边形外的部分都是确定的，而这些多边形的部分互相独立。可以这样构造：

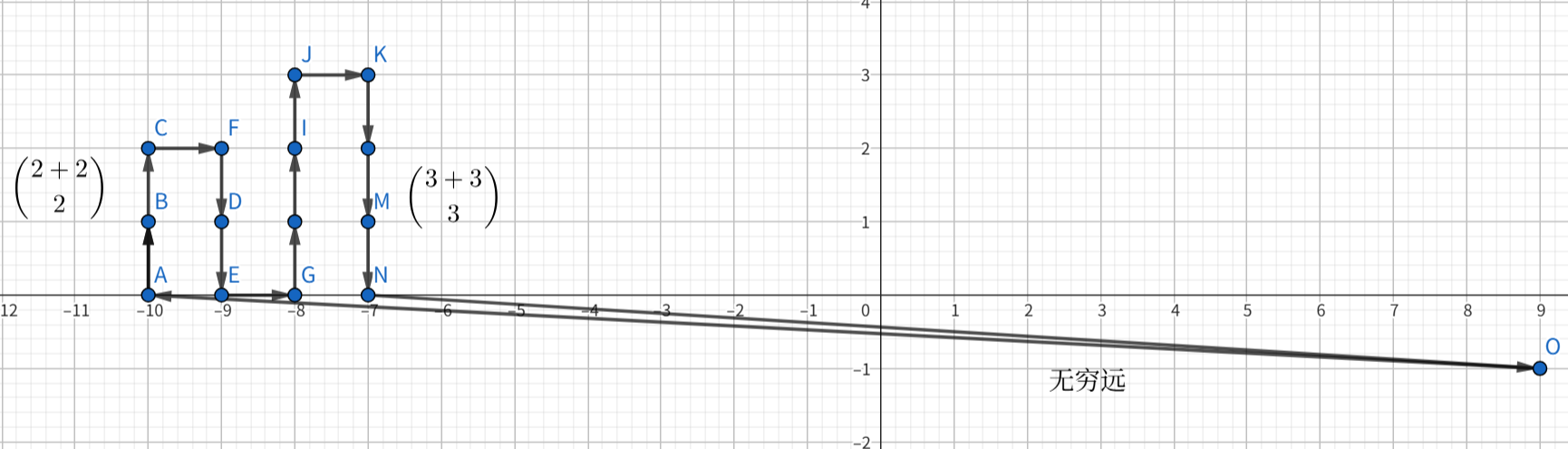
注意到三角剖分中必然包含三角形 ANO，否则便会违背三角形不能有点以外的相交的限制

因此，可以把若干个组合数形式的 用 个点合并。直接使用

记 。这种方法使用的点的数量是 的。超出了限制范围。

观察到

的构造是前面的内容。左右是两个规模更小的子问题。取 分治解决即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<bits/stdc++.h>
#define f(i,x,y) for(int i=x, i##end=y; i<=i##end; ++i)
#define d(i,x,y) for(int i=y, i##end=x; i>=i##end; --i)
#define uf(i,x,y) for(int i=x, i##end=y; i<i##end; ++i)
#define ll long long
#define pir pair<int, int>
#define fir first
#define sec second
#define mp make_pair
#define pb push_back 
char ch;
int rd() {
	int f=1, x=0; ch=getchar();
	while(!isdigit(ch)) { f=((ch=='-')?-1:f); ch=getchar(); }
	while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar(); }
	return x*f;
}
void rd(int& x) { x=rd(); }
using namespace std;
const int _ = 10, __ = 334, inf = 1000000;
int n, a[_], c[_], tot = 0, nowx = 0, x[__], y[__];
void build(int l, int r) {
	if(l == r) return ;
	int mid = (l+r)>>1;
	int sl, sr = sl = 0;
	f(i,l,mid) sl += a[i]; f(i,mid+1,r) sr += a[i];
	f(i,0,sl) x[++tot] = nowx, y[tot] = i; ++nowx;
	d(i,0,sr) x[++tot] = nowx, y[tot] = i; ++nowx;
	if(r == l + 1) return ;
	build(l, mid); build(mid+1, r);
}
int main() {
	rd(n); f(i,1,n) rd(a[i]);
	build(1, n);
	cout << tot + 1 << endl;
	f(i,1,tot) cout << x[i] << ' ' << y[i] << '\n' ;
	cout << inf << ' ' << -1 << endl;
	return 0;
}
≡